Chapter 9 Complex surveys

By the end of this chapter you will know how to:

  • Setup a survey object using complex survey information such as sampling weight and stratification variables.
  • Use a tidyverse-esq approach for descriptive statistics.
  • Fit a GLM (logistic).

We will use the survey package and a tidyverse-style wrapper called srvyr.

library(survey)
library(srvyr)

9.1 Readings

These are handy:

9.2 The dataset

This chapter’s dataset is drawn from the 2011 Canadian National Election Study – taken from the carData package and described by the Fox and Weisberg appendix cited above. Download it here.

There are 2231 observations on the following 9 variables:

Variable name Description
id Household ID number.
province a factor with (alphabetical) levels AB, BC, MB, NB, NL, NS, ON, PE, QC, SK; the sample was stratified by province.
population population of the respondent’s province, number over age 17.
weight weight sample to size of population, taking into account unequal sampling probabilities by province and household size.
gender a factor with levels Female, Male.
abortion attitude toward abortion, a factor with levels No, Yes; answer to the question “Should abortion be banned?”
importance importance of religion, a factor with (alphabetical) levels not, notvery, somewhat, very; answer to the question, “In your life, would you say that religion is very important, somewhat important, not very important, or not important at all?”
education a factor with (alphabetical) levels bachelors (Bachelors degree), college (community college or technical school), higher (graduate degree), HS (high-school graduate), lessHS (less than high-school graduate), somePS (some post-secondary).
urban place of residence, a factor with levels rural, urban.

Read in the data.

ces <- read.csv("ces11.csv", stringsAsFactors = TRUE)

I’m setting stringsAsFactors to TRUE so that the variables which are obviously factors are setup accordingly (R used to this by default; sometimes it had irritating side-effects).

9.3 The components of a survey design

The key parts of the dataset which describe the survey design are as follows:

ces %>% select(id, province, population, weight) %>%
  head(6)
##     id province population  weight
## 1 2851       BC    3267345 4287.85
## 2  521       QC    5996930 9230.78
## 3 2118       QC    5996930 6153.85
## 4 1815       NL     406455 3430.00
## 5 1799       ON    9439960 8977.61
## 6 1103       ON    9439960 8977.61
  • id is a unique identifier for each individual, which is particularly important when there is more than one data point per person, e.g., for multilevel modelling (not in this dataset).
  • province the data were stratified by province – random sampling by landline numbers was done within province.
  • population provides the population by province.
  • weight is the sampling weight, in this dataset calculated based on differences in province population, the study sample size therein, and household size.

Here is how to setup a survey object using srvyr:

ces_s <- ces %>%
  as_survey(ids = id,
            strata = province,
            fpc = population,
            weights = weight)

9.4 Describing the data

We will sometimes want to compare weighted and unweighted analyses. Here is a warmup activity to show how using the tidyverse.

9.4.1 Activity

  1. use the ces data frame and tidyverse to calculate the number of people who think abortion should be banned
  2. do the same again, but this time use the ces_s survey object created above – what do you notice?
  3. compare the proportions saying yes by group

Hint: you will want to use group_by.

Another hint: to count, use the function n. The version for survey objects is called survey_total.

9.4.2 Answer

a. use the ces data frame and tidyverse to calculate the number of people who think abortion should be banned

ces %>%
  group_by(abortion) %>%
  summarise(n = n())
## `summarise()` ungrouping output (override with `.groups` argument)
## # A tibble: 2 x 2
##   abortion     n
##   <fct>    <int>
## 1 No        1818
## 2 Yes        413

b. do the same again, but this time use the ces_s survey object created above – what do you notice?

ces_s %>%
  group_by(abortion) %>%
  summarise(n = survey_total())
## # A tibble: 2 x 3
##   abortion         n    n_se
##   <fct>        <dbl>   <dbl>
## 1 No       13059520. 196984.
## 2 Yes       2964018. 162360.

The counts are much bigger than the number of rows in the dataset due to the sampling weights.

c. compare the proportions saying yes by group

One way to do this is by copy and paste!

Unweighted:

prop_unweighted <- 413 / (413 + 1818)
prop_unweighted
## [1] 0.1851188

Weighted:

prop_weighted <- 2964018 / (2964018 +   13059520)
prop_weighted
## [1] 0.184979

The unweighted proportion of “yes” is only a little different in this case: 0.1851188 (unweighted) v 0.184979 (weighted).

Here’s how to answer the questions in one go:

ces_s %>%
  group_by(abortion) %>%
  summarise(n_raw = unweighted(n()),
            n_weighted = survey_total()) %>%
  mutate(prop_raw = n_raw / sum(n_raw),
         prop_weighted = n_weighted / sum(n_weighted)) %>%
  select(-n_weighted_se)
## # A tibble: 2 x 5
##   abortion n_raw n_weighted prop_raw prop_weighted
##   <fct>    <int>      <dbl>    <dbl>         <dbl>
## 1 No        1818  13059520.    0.815         0.815
## 2 Yes        413   2964018.    0.185         0.185

9.5 Fitting a GLM

The survey package makes this very easy. There is a command called svyglm which is identical to glm except it has parameter called design instead of data.

See ?svyglm

9.5.1 Activity

  1. mutate the survey object to add a binary variable called againstAbortion which is 1 if the participant is against abortion and 0 if not.
  2. fit an intercept-only logistic regression model without using weights (you can use as_tibble to get the “raw” data frame hidden within the survey object).
  3. Do the same again, this time using the survey structure.
  4. compare the predicted proportions with the “raw” proportions we calculated earlier

9.5.2 Answer

a. mutate the survey object to add a binary variable called againstAbortion which is 1 if the participant is against abortion and 0 if not.

ces_s <- ces_s %>%
  mutate(againstAbortion = as.numeric(ces$abortion == "Yes"))

b. fit an intercept-only logistic regression model without using weights (you can use as_tibble to get the “raw” data frame hidden within the survey object).

m0 <- glm(againstAbortion ~ 1,
          data = as_tibble(ces_s),
          family = binomial)
summary(m0)
## 
## Call:
## glm(formula = againstAbortion ~ 1, family = binomial, data = as_tibble(ces_s))
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -0.6399  -0.6399  -0.6399  -0.6399   1.8367  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -1.48204    0.05451  -27.19   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 2137.6  on 2230  degrees of freedom
## Residual deviance: 2137.6  on 2230  degrees of freedom
## AIC: 2139.6
## 
## Number of Fisher Scoring iterations: 4

c. Do the same again, this time using the survey structure.

sm0 <- svyglm(againstAbortion ~ 1, design = ces_s,
              family = binomial)
## Warning in eval(family$initialize): non-integer #successes in a binomial glm!
summary(sm0)
## 
## Call:
## svyglm(formula = againstAbortion ~ 1, design = ces_s, family = binomial)
## 
## Survey design:
## Called via srvyr
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -1.48297    0.06534   -22.7   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1.000448)
## 
## Number of Fisher Scoring iterations: 4

d. compare the predicted proportions with the “raw” proportions we calculated earlier

This undoes the log-odds (logit) transform:

exp(coef(m0)) / (1+exp(coef(m0)))
## (Intercept) 
##   0.1851188
exp(coef(sm0)) / (1+exp(coef(sm0)))
## (Intercept) 
##    0.184979

The answer is the same as for the simple unweighted and weighted proportions, respectively.

9.6 Slopes

Now, having completed the traditional step of fitting an intercept-only model, we can give the slopes a go.

The Anova command in the car package works for svyglm models as before.

9.6.1 Activity

Regress againstAbortion on importance, education, and gender, and interpret what you find.

9.6.2 Answer

sm1 <- svyglm(againstAbortion ~ importance + education + gender,
              design = ces_s,
              family = binomial)
## Warning in eval(family$initialize): non-integer #successes in a binomial glm!
summary(sm1)
## 
## Call:
## svyglm(formula = againstAbortion ~ importance + education + gender, 
##     design = ces_s, family = binomial)
## 
## Survey design:
## Called via srvyr
## 
## Coefficients:
##                    Estimate Std. Error t value Pr(>|t|)    
## (Intercept)         -3.8204     0.2962 -12.897  < 2e-16 ***
## importancenotvery    0.4606     0.3481   1.323   0.1858    
## importancesomewhat   1.3287     0.2715   4.894 1.06e-06 ***
## importancevery       3.1405     0.2619  11.993  < 2e-16 ***
## educationcollege     0.4452     0.2278   1.954   0.0508 .  
## educationhigher      0.3301     0.3046   1.084   0.2786    
## educationHS          0.5692     0.2269   2.508   0.0122 *  
## educationlessHS      1.0307     0.2468   4.177 3.07e-05 ***
## educationsomePS      0.1439     0.2806   0.513   0.6081    
## genderMale           0.3299     0.1482   2.225   0.0261 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 0.973961)
## 
## Number of Fisher Scoring iterations: 5

To interpret those categorical predictors, it will help to check what the levels are:

levels(ces$importance)
## [1] "not"      "notvery"  "somewhat" "very"

So “not” is the comparison level.

levels(ces$education) 
## [1] "bachelors" "college"   "higher"    "HS"        "lessHS"    "somePS"

“bachelors” is the comparison level.

Gender is just a binary.

Example interpretations:

  • Men were more likely to be against abortion (log-odds 0.33 more)

  • People for whom religion was very important were more likely than those who said “not important at all” to be against abortion (log-odds 3.14)

You could get the odds ratios like so:

exp(coef(sm1)) %>% round(2)
##        (Intercept)  importancenotvery importancesomewhat     importancevery 
##               0.02               1.59               3.78              23.12 
##   educationcollege    educationhigher        educationHS    educationlessHS 
##               1.56               1.39               1.77               2.80 
##    educationsomePS         genderMale 
##               1.15               1.39

So the odds ratio of “very” versus “not” important is 23.1.

The ggeffects package also works with survey models (hurrah):

library(ggeffects)
ggeffect(sm1, terms = c("education", "importance"))  %>%
  plot() +
  ylim(0,1)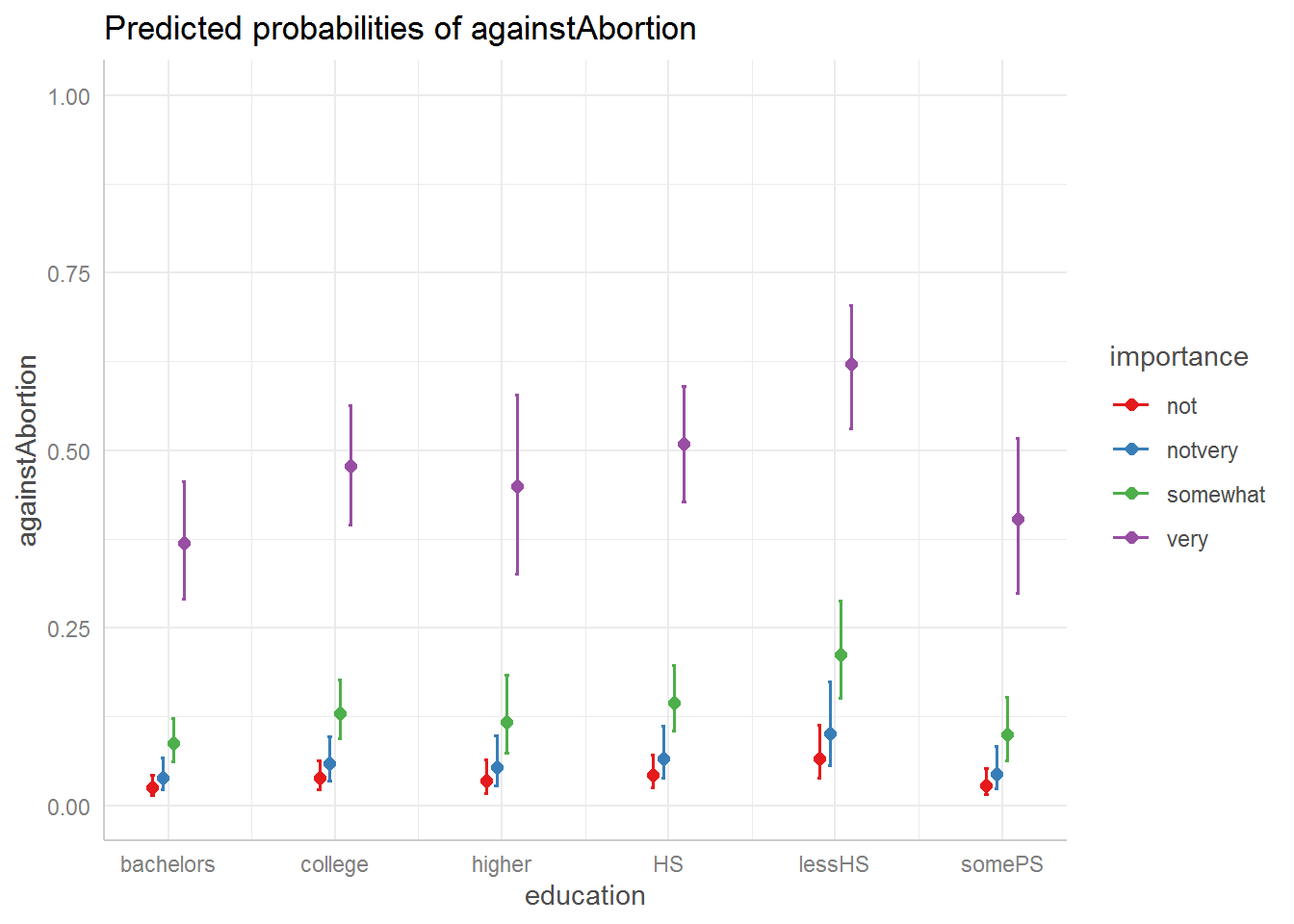

9.7 Diagnostics

Many of the diagnostic checks we previously encountered work here too.

Here are the VIFs:

vif(sm1)
##                GVIF Df GVIF^(1/(2*Df))
## importance 1.052799  3        1.008612
## education  1.066741  5        1.006482
## gender     1.039299  1        1.019460

My favorite, the DFBETA plots:

dfbetaPlots(sm1)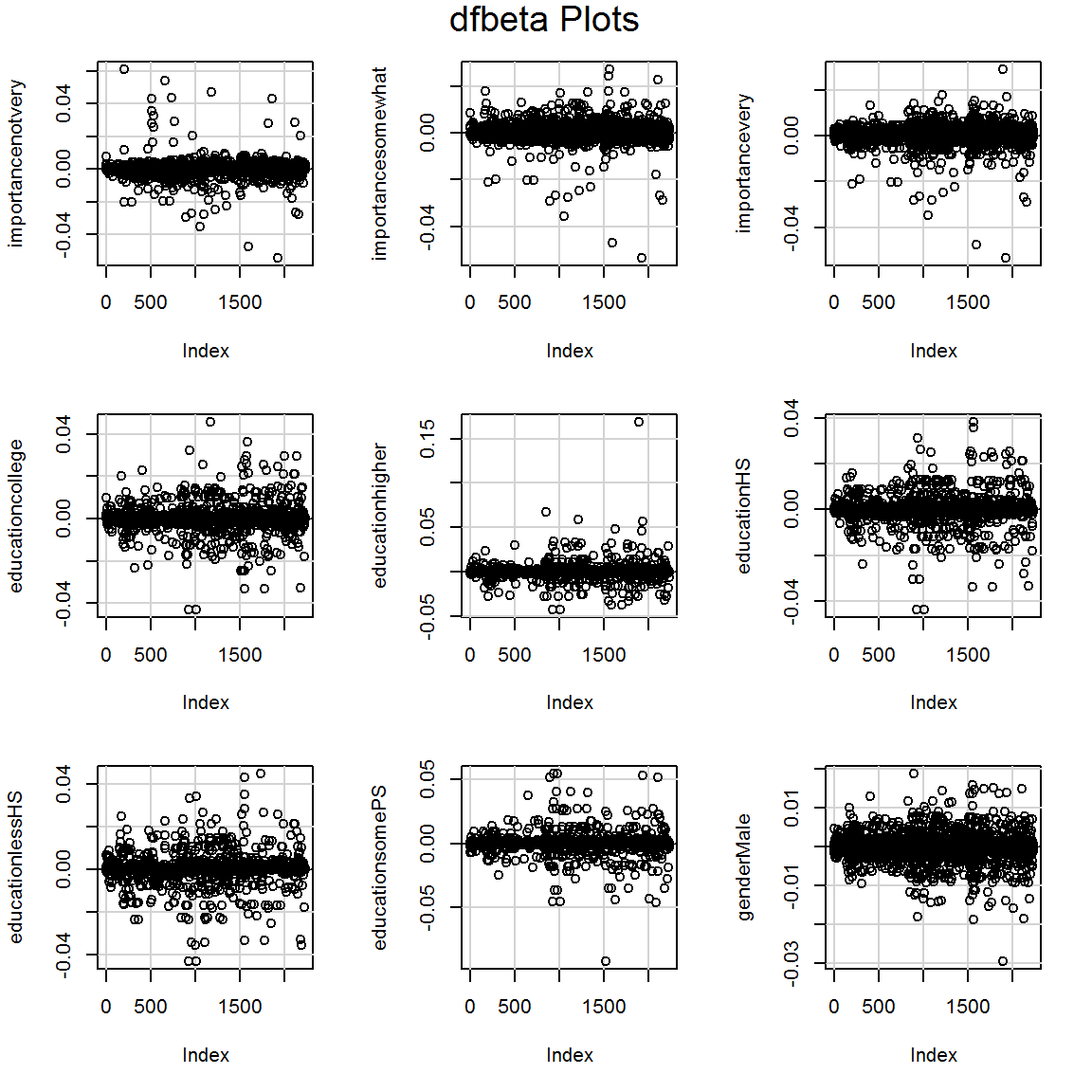

Try also:

influence.measures(sm1)

9.8 Another worked example: the European Social Survey

NatCen recently published analyses of views on fairness and justice in Britain (Curtice, Hudson, & Montagu, 2020), using data from the ninth wave of the 2019 European Social Survey (European Social Survey Round 9 Data, 2018).

Let’s see if we can replicate the results.

Firstly, you will have to download the data from the ESS website. Go for the SPSS version. (You will have to register but it is a very quick process.) It will arrive as a zip file (ESS9e02.spss.zip). Simply extract the SPSS file therein (ESS9e02.sav) and move it to the same folder as your Markdown file.

library(haven)
ess9 <- read_sav("ESS9e02.sav")

Try having a look:

View(ess9)

Okay, if that has worked then the next problem is finding the variables we want to analyse!

The report opens with a spotlight figure:

Only 20% of the British public think that differences in wealth in Britain are fair, whilst a majority (59%) think that wealth differences in Britain are unfairly large and a further 16% think that differences in wealth are unfairly small.

The question asked was:

In your opinion, are differences in wealth in Britain unfairly small, fair, or unfairly large?

It’s a good exercise to spend some time wading through the documentation on the ESS website to find the variable name, before looking at the answer below…

We will also need the variable for country (easier to spot) and any information required for setting up the survey object. The ESS website helpfully advises:

In general, you must weight tables before quoting percentages from them. The Design weights (DWEIGHT) adjust for different selection probabilities, while the Post-stratification weights (PSPWGHT) adjust for sampling error and non-response bias as well as different selection probabilities. Either DWEIGHT or PSPWGHT must always be used. In addition, the Population size weights (PWEIGHT) should be applied if you are looking at aggregates or averages for two or more countries combined. See the guide Weighting European Social Survey Data for fuller details about which weights to use.

This also links to a guide to weighting the data.

It’s also worth printing all the variable names – if only to spot that they have ended up in lower case.

9.8.1 Set up the survey object

First, I’m going to fix the country variable. It currently looks like:

table(ess9$cntry)
## 
##   AT   BE   BG   CH   CY   CZ   DE   EE   ES   FI   FR   GB   HR   HU   IE   IT 
## 2499 1767 2198 1542  781 2398 2358 1904 1668 1755 2010 2204 1810 1661 2216 2745 
##   LT   LV   ME   NL   NO   PL   PT   RS   SE   SI   SK 
## 1835  918 1200 1673 1406 1500 1055 2043 1539 1318 1083

But the dataset also has nicer labels included, which we can get like this using the as_factor function (note the underscore). This function is in the haven package.

ess9$cntry <- as_factor(ess9$cntry, levels = "labels")
table(ess9$cntry)
## 
## United Kingdom        Belgium        Germany        Estonia        Ireland 
##           2204           1767           2358           1904           2216 
##     Montenegro         Sweden       Bulgaria    Switzerland        Finland 
##           1200           1539           2198           1542           1755 
##       Slovenia       Slovakia    Netherlands         Poland         Norway 
##           1318           1083           1673           1500           1406 
##         France        Croatia          Spain         Serbia        Austria 
##           2010           1810           1668           2043           2499 
##          Italy      Lithuania       Portugal        Hungary         Latvia 
##           2745           1835           1055           1661            918 
##         Cyprus        Czechia 
##            781           2398

Now let’s setup the survey object:

ess9_survey <- ess9 %>%
  as_survey_design(ids = idno,
                   strata = cntry,
                   nest = TRUE,
                   weights = pspwght)

The nest option takes account of the ids being nested within strata: in other words the same ID is used more than once across the dataset but only once in a country.

9.8.2 Try the analysis

The country variable is cntry and the wealth variable is wltdffr, which I spotted with the help of the code book.

The first thing you will spot is that the original variable is coded from -4 to 4:

Code Meaning
-4 Small, extremely unfair
-3 Small, very unfair
-2 Small, somewhat unfair
-1 Small, slightly unfair
0 Fair
1 Large, slightly unfair
2 Large, somewhat unfair
3 Large, very unfair
4 Large, extremely unfair

So let’s create another variable which is grouped as per the NatCen report:

ess9_survey <- ess9_survey %>%
  mutate(wltdffr_group =
           case_when(
             wltdffr >= -4 &
               wltdffr <= -1 ~ "Unfairly small",
             wltdffr == 0 ~ "Fair",
             wltdffr >= 1 & wltdffr <= 4 ~ "Unfairly large"
           ),
         wltdffr_group = factor(wltdffr_group,
                                  levels = c("Unfairly small",
                                             "Fair",
                                             "Unfairly large"))
  )
gb_wealth <- ess9_survey %>%
  filter(cntry == "United Kingdom") %>%
  group_by(wltdffr_group) %>%
  summarise(prop = survey_mean(vartype = "ci"))
gb_wealth 
## # A tibble: 4 x 4
##   wltdffr_group    prop prop_low prop_upp
##   <fct>           <dbl>    <dbl>    <dbl>
## 1 Unfairly small 0.164    0.146    0.181 
## 2 Fair           0.196    0.176    0.216 
## 3 Unfairly large 0.589    0.565    0.613 
## 4 <NA>           0.0508   0.0401   0.0615

The results are the same as per the report. Let’s round to show this more clearly:

gb_wealth %>%
  mutate(perc = (prop*100) %>% round(0)) %>%
  select(wltdffr_group, perc)
## # A tibble: 4 x 2
##   wltdffr_group   perc
##   <fct>          <dbl>
## 1 Unfairly small    16
## 2 Fair              20
## 3 Unfairly large    59
## 4 <NA>               5

We can also plot the results:

gb_wealth %>%
  filter(!is.na(wltdffr_group)) %>%
  ggplot(aes(x = wltdffr_group, y = prop*100)) +
  geom_col(fill = "#B053A1") +
  geom_errorbar(aes(ymin = prop_low*100,
                    ymax = prop_upp*100), width = 0.2) +
  ylim(0,100) +
  labs(y = "%", x = NULL,
       title = "In your opinion, are differences in wealth in Britain\nunfairly small, fair, or unfairly large?")

Let’s do it again for a selection of countries. First, make a function which carries out the analysis for one country:

gimme_country_results <- function(the_cntry) {
  ess9_survey %>%
    filter(cntry == the_cntry) %>%
  group_by(wltdffr_group) %>%
  summarise(prop = survey_mean(vartype = "ci")) %>%
  mutate(cntry = the_cntry)
}

Check it works for the UK:

gimme_country_results("United Kingdom")
## # A tibble: 4 x 5
##   wltdffr_group    prop prop_low prop_upp cntry         
##   <fct>           <dbl>    <dbl>    <dbl> <chr>         
## 1 Unfairly small 0.164    0.146    0.181  United Kingdom
## 2 Fair           0.196    0.176    0.216  United Kingdom
## 3 Unfairly large 0.589    0.565    0.613  United Kingdom
## 4 <NA>           0.0508   0.0401   0.0615 United Kingdom

Run it for all the countries of interest:

conts <- c("Germany", "Spain", "France", "United Kingdom", "Italy")
euro_wealth <- map_dfr(conts, gimme_country_results)
head(euro_wealth)
## # A tibble: 6 x 5
##   wltdffr_group    prop prop_low prop_upp cntry  
##   <fct>           <dbl>    <dbl>    <dbl> <chr>  
## 1 Unfairly small 0.261    0.241    0.281  Germany
## 2 Fair           0.121    0.106    0.135  Germany
## 3 Unfairly large 0.557    0.535    0.579  Germany
## 4 <NA>           0.0619   0.0508   0.0730 Germany
## 5 Unfairly small 0.212    0.192    0.232  Spain  
## 6 Fair           0.0698   0.0575   0.0822 Spain

Next, try a plot:

euro_wealth %>%
  filter(!is.na(wltdffr_group)) %>%
  ggplot(aes(x = cntry,
             y = prop*100,
             ymin = prop_low*100,
             ymax = prop_upp*100,
             fill = wltdffr_group)) +
  geom_col(position = position_dodge(width = .8), width = 0.6) + 
  geom_errorbar(position=position_dodge(width = .8),
                colour="black",
                width = 0.2) +
  ylim(0,100) +
  labs(y = "%", x = NULL,
       title = "In your opinion, are differences in wealth\nunfairly small, fair, or unfairly large?",
       fill = NULL)